Trivia useful for puzzles

Authoring Story Research and Design
21

The Tower of Hanoi with 4 pegs instead of 3 was only completely solved in 2018. The word “solved” here means to find a closed expression for Wₙ, the minimum number of moves necessary to transfer a tower of n discs between two pegs, using two auxiliary pegs, under the usual Tower of Hanoi rules. It is easy to prove that

eq1

where Tₙ=2ⁿ-1 is the number of moves necessary to solve a 3-peg Tower of Hanoi. In 1941, an algorithm was independently devised by mathematicians J.S. Frame and B.M Stewart, which consists on transferring first a triangular number of discs to a peg, then moving the largest remaining disks without altering that secondary tower, then moving the initial tower again, which gives the expression above. The bound is indeed optimal, so the expression is actually an equality, but this was not completely proven until Roberto Demontis found a proof in 2018. The problem had eluded solution for more than a century.

The generalized Tower of Hanoi with any number of auxiliary pegs can be solved optimally this way: If Zₖ(n) is the minimum number of moves necessary to transfer n discs with k pegs, we have

eq2

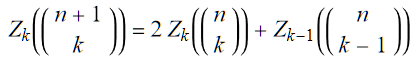
where the quantities between brackets are the binomial coefficients
eq3

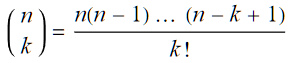
This means, for example, that a Tower of Hanoi problem with 4 pegs and n(n+1)/2 discs can be solved in exactly 2ⁿ(n-1)+1 moves. In particular, a problem with 6 discs and 4 pegs can be solved in 17 moves.

7 Likes
22

This one’s definitely got puzzle potential!

Brb, adding a thirst daemon to my four-peg Tower of Hanoi puzzle to kill the player if they take too many moves…

7 Likes
23

Music puzzles are interesting and have been done before in games (there was one in Hogwarts Legacy, which was the last one I remember) but I think in an IF context, the note values would be most useful in forming a puzzle.

Note values give you the relative duration of a given note. The duration varies with the tempo (speed), which varies with the piece and the player/conductor. A note value can be dotted, which adds half the value to the duration (1.5x). It can also be double-dotted, which adds another fourth to the duration (1.75x). Tied notes have the same pitch and allow durations not aligning to the set values. Each note also has a corresponding rest of equal duration, in which the instrument is not played.

Most beat lengths are quarter notes/crochets, so relative value is done based on that as “1”, although you could also establish a whole note/semibreve as “1”, which gives you the American names (with the assumption that a whole note = 4).

Relative value American name British name
length of measure whole note/rest semibreve
2 half note minim
1 quarter note crochet/semiminim
1/2 eighth note quaver
1/4 sixteenth note semiquaver
1/8 thirty-second note demisemiquaver
4 Likes
24

There’s been a bit of inflation in the note values over time, which is why the longest note in the British system is known as the “semibreve”—Italian for “half of a short”—and the standard unit now is the “minim”—Italian for “shortest”!

The larger values are the “breve” (“short”), or double whole note, the “longa” (“long”), or quadruple whole note, and the “maxima” (“longest”), or octuple whole note, but nobody uses those any more if they can help it. This is why I think the American names make more sense nowadays!

And if you really want, you can get even shorter and use a hemisemidemiquaver, or sixty-fourth note. Vivaldi once used a 256th note, which I think is about the shortest that can reasonably be played. I don’t think even Liszt went further than that, though he once used a quadruple-dotted note, which has 1.9375 times its normal duration (1+1/2+1/4+1/8+1/16)!

2 Likes
25

The Metonic Cycle is a period of 19 years after which the phases of the Moon repeat on the same calendar dates. It was described by the ancient Greek astronomer Meton of Athens around 432 BC. The cycle works because 19 solar years are almost exactly equal to 235 lunar months (approximately 6939.75 days). This was used in both Greek and Babylonian calendars to align the lunar and solar years, and it still forms part of both the lunisolar Hebrew calendar and the timing of Easter in the Christian liturgical calendar.

The Saros Cycle is a period of approximately 18 years, 11 days, and 8 hours after which nearly identical solar and lunar eclipses occur. This is based on the alignment of three different cycles:

  • The synodic month (New Moon to New Moon): ~29.53 days;
  • The draconic month (Node to Node, where the Moon crosses the Earth’s orbital plane): ~27.21 days; and
  • The anomalistic month (Perigee to Perigee, the Moon’s closest point to Earth): ~27.55 days.

These cycles sync approximately every 18 years, leading to a repeat in eclipse geometry. This was known, among others, to ancient Babylonians, which used it to predict eclipses.

It is believed that the Antikythera mechanism was an analogical device to calculate astronomical alignment events according to the above cycles. It does not take a lot of imagination to devise some puzzles around these topics…

3 Likes
26

There’s an idea for an unusual mechanic in a parser game:

Typing the leters Athrough G followed by a single digit number plays the tone corresponding to that note, and typing multiple notes on the same line plays a melody. A simple version could be like the Ocarina of Time from Zelda(though there you could just have one octave worth of notes, but maybe the player can summon magic keyboards a la Cure Muse and Otokichi from Suite Precure and you have the entire range of the piano. In either case, you could find sheet music items in game that act like spells when played on your magical musical instrument or have a variety of sound based puzzles… No idea how to make harmony or different note durations parsable though… though, is using a mix of wholes, doubles, and quadruples fundamentally different from a mix of quarters, halves, and wholes? Can’t you convert one to the other simply by quartering or quadrupling the tempo?

I knew about the 19 year long term cycle of the moon… though it just occurred to me that the equinoxes, solstices, and cross quarter days, while often observed on 3/21, 9/21, 6/21, 12/21, 2/2, 5/1, 8/1, and 10/31 actually vary by a few days year to year, so it raises the question of how often a given moon phase falls on a given quarter/cross-quarter day if we’re talking the actual dates of the relevant astronomical events and not the dates they are observed on.

Also, could you imagine trying to work out Jovian months? Or even just eclipses on Mars.

1 Like
27

That’s basically what Hogwarts Legacy does. There’s a paper somewhere with the sheet music to the opening of Hedwig’s Theme, and an indication that the staff (lines) correspond to bells. There’s a location where those bells are located, with bells on both the lines and spaces. Using a basic long-range attack spell, you hit the bells in succession (rhythm does not matter) to solve the puzzle.

No, but the whole note being the longest note (taking up the whole measure) is much more common.

2 Likes
28

Clearly this could be complicated by having the instruments and the sheets use different scales. For example, the music sheets are in 24-EDO and 9-EDO, but the only instrument you have access to is in 72-EDO (a superset of both).

29

What is heavier, a pound of feathers or a pound of gold? The right answer is a pound of feathers. However, if we ask:

What is heavier, an ounce of feathers or an ounce of gold? The right answer is then an ounce of gold.

This is because the weight of precious metals is measured in Troy units, while the weight of anything else is measured in Avoirdupois units. The words “ounces” and “pounds” have a complete different meaning when used with bullion.

The region of Champagne in France was quite lively in the 12th century under the rule of the local Counts, who prospered from hosting some of the largest market Fairs in western Europe. Merchants from across the continent gathered in the city of Troyes to trade their wools, silks, leathers, furs, spices, and, of course, precious gold and silver wares. In order to regulate commerce, rules were introduced governing the efficient operation of the Fairs.

By the late 12th century, the Troy weight system was widely adopted as the foundation of various European monetary systems. It was introduced to Britain during the reign of King Henry II (1154–1189), an Angevin ruler who also governed extensive regions in France.

English pennies, valued at 1/240th of a pound sterling, were designed to weigh 1/240th of a Troy pound of sterling silver. With 20 “pennyweights” making up one Troy ounce, a Troy pound consisted of 12 Troy ounces.

Although the Avoirdupois system (where a pound equals 16 ounces) became the standard for general goods, Troy weights continued to be used for measuring and pricing precious metals.

While Troy pounds and pennyweights largely fell out of use in the 19th century, The Troy ounce endured. Even when British law eliminated many traditional weights and measures in 1963, the Troy ounce was preserved for the trade of precious metals.

So: there are 12 Troy ounces in every Troy pound and 16 ounces in every Avoirdupois pound. Troy ounces are heavier than ounces, but troy pounds are lighter than pounds. Comparing the two systems by way of the metric system for clarity:

Troy Ounces (ozt.) > Avoirdupois Ounces (oz.)

1 Troy ounce = 31.1035 grams
1 Avoirdupois ounce = 28.3495 grams
With a difference of 2.754 grams, a Troy ounce is around 10% heavier

Troy Pounds (lbt.) < Avoirdupois Pounds (lb.)

1 Troy pound = 12 Troy ounces = 373.242 grams
1 Avoirdupois pound = 16 Avoirdupois ounces = 453.592 grams
With a difference of 80.35 grams, a Troy pound is lighter by 2.83 Avoirdupois ounces.
9 Likes
30

The oldest known pocket timepiece predates the Norman invasion!

472373119_1009039864591539_3509639167533470847_n
472373119_1009039864591539_3509639167533470847_n1080×681 55.4 KB

This tenth-century Anglo-Saxon “pocket sundial” was discovered at Canterbury Cathedral. You put the gnomon pin in the hole for the appropriate month (the other six months are on the other side), then suspend it from the chain to ensure it’s fully vertical. The tip of the shadow will meet the lower dot at noon, and the upper dot at 3pm and 9am.

Apparently Canterbury used to sell replicas, but they no longer do. So I’m contemplating how difficult it would be to make one myself, for my latitude…

8 Likes
31

“The Roman gnomes?”
“No, man, gnomon! The shadow-casty part of a sundial, you gnomon?”
“Stop gno-monopolizing the jokes!”
“Can’t help it, it’s gnomon-stop.”
“That…was a stretch. That was terrible.”
“Well, there’s gnomon place to go but up.”

6 Likes
32

And as a bonus: If you don’t know the directions (north etc.) you can calculate them from that sundial.

1 Like
33

And related to the other type of compass:

The only regular n-gons constructible with compass and straight edge alone are those for where n is a power of 2, a Fermat Prime, a product of distinct Fermat primes, or a product of distinct Fermat primes and a power of 2. Fermat primes are those that are 1 more than a power of 2, of which there are 5 known: 3, 5, 17, 257, and 65537 with it being an open problem whether there are any more.

As such, a regular heptagon is the smallest regular n-gon for which a pure compass and straightedge construction is impossible. However, the heptagon is constructible with the use of angle trisector, as well as via origami, though I know not whether the two tools are equal in constructive power. Interestingly, the tomahawk, a tool for angle trisection, can be constructed with compass and straightedge, but this does not violate the impossibility of trisecting angles with compass and streight edge as a tomahawk thus contructed cannot be moved freely. There is a special type of prime associated with regular n-gons constructible with compass, straightedge, and angle trisector, but I forget what they are called and what their special properties are.

A hendecagon is the smallest regular polygon not constructible with compass, straightedge, and angle trisector, though it can be constructed with neusis.

A regular 23-gon is the smallest regular n-gon that cannot be constructed with neusis, though there are special curves that can be employed in its construction.

3 Likes
34

They are not; origami is more powerful. Paper folding allows constructing all points expressible as roots of polynomials of degree 4, while an angle trisector is limited to degree 3.

Since you’re interested, the constructible regular polygons using origami are those whose number of sides is the product of a power of 2, a power of 3, and any product of Pierpont primes. Pierpont primes include Fermat primes, so this set includes all straightedge + compass constructions and all cubic section constructions as well.

See also Mascheroni constructions as a curiosity that goes in the opposite direction: just a single compass, which sometimes can’t even be changed angle (called a “rusty” compass). The topic of restricted geometrical constructions was very en vogue in the 19th century and part of mainstream mathematics; today is extremely niche and limited to recreational pursuits, but there’s plenty of material there still to be fully explored.

1 Like