After several failed attempts, I was finally able to code a working example for this. Your mileage may vary 
Big thanks to @Draconis for insight on using recursive calls to spread the points!
The scene is the Demo room containing a number of points as the OP stated in the initial question. To interact with the points you can say ‘compare point_name to point_name’, ‘examine point_name’, or ‘debug map’. I ran through several test scenarios. Cases where multiple points occupy the same physical X/Y coordinates are handled. Cases where multiple disconnected groups of 2D point collections have been defined are also handled. The root of each discrete collection of 2D points is randomly selected and the mapping out of the points performed when game play begins. Here is the code:
[Setup a demo room for our points to exist in]
Demo is a room. The description is "In this demo of 2D points you can type 'debug map', 'examine <point name>', or 'compare <point name> to <point name>' to see more information about the 2d point environment.".
[Define relations and verbs to use with points]
Leftness relates various things to various things.
The verb to be left of means the leftness relation.
The verb to be right of means the reversed leftness relation.
Atopness relates various things to various things.
The verb to be atop means the atopness relation.
The verb to be under means the reversed atopness relation.
[Define properties of a point]
A point is a kind of thing.
A point has a number called the y-value.
A point has a number called the x-value.
A point can be mapped or unmapped. Points are usually unmapped.
A point can be root or notroot. Points are usually notroot.
The y-value of a point is usually 0.
The x-value of a point is usually 0.
[Define some points in the demo room]
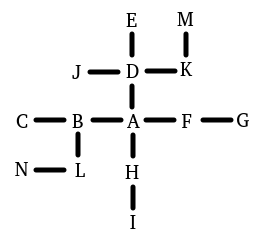
point_a, point_b, point_c, point_d, point_e, point_f, point_g, point_h, point_i, point_j, point_k, point_l, point_m and point_n are points in Demo.
[Orient the points]
point_a is right of point_b.
point_b is right of point_c.
point_d is atop point_a.
point_e is atop point_d.
point_f is right of point_a.
point_g is right of point_f.
point_h is under point_a.
point_i is under point_h.
point_j is left of point_d.
point_k is right of point_d.
point_l is under point_b.
point_m is atop point_k.
point_n is left of point_l.
[Spread values through the map from the root recursively per Draconis]
To spread values from (P - a point):
now P is mapped;
while an unmapped point (called Q) is atop P:
now the x-value of Q is the x-value of P;
now the y-value of Q is the y-value of P plus one;
spread values from Q;
while an unmapped point (called Q) is under P:
now the x-value of Q is the x-value of P;
now the y-value of Q is the y-value of P minus one;
spread values from Q;
while an unmapped point (called Q) is left of P:
now the y-value of Q is the y-value of P;
now the x-value of Q is the x-value of P minus one;
spread values from Q;
while an unmapped point (called Q) is right of P:
now the y-value of Q is the y-value of P;
now the x-value of Q is the x-value of P plus one;
spread values from Q;
[Before the game begins dynamically generate the 2D point map using a random root]
When play begins:
while an unmapped point is anywhere:
let P be a random unmapped point;
now P is root;
spread values from P;
[Implement examination of a point]
Instead of examining a point (called temp):
let item_i be a point;
let item_i be temp;
let J be the list of points;
repeat with item_j running through J:
say "[item_i] is [if item_i is left of item_j] left [otherwise if item_i is right of item_j] right [otherwise] neither right nor left [end if] of [item_j].[line break]";
say "[item_i] is [if item_i is atop item_j] atop [otherwise if item_i is under item_j] under [otherwise] neither atop nor under [end if] of [item_j].[line break]";
say "[line break]";
[Implement examination the 2d point map]
Mapdebugging is an action applying to nothing.
Understand "debug map" as mapdebugging.
Instead of mapdebugging:
let J be the list of points;
repeat with item_j running through J:
let B be the y-value of item_j;
let A be the x-value of item_j;
say "[item_j] : x-value = [A], y-value = [B]";
if item_j is root:
say " *** ROOT ***";
say "[line break]";
say "[line break]".
[Implement point to point comparison]
Comparing is an action applying to two things.
Understand "compare [something] to [something]" as comparing.
Instead of comparing:
let item_i be a point;
let item_i be the noun;
let item_j be a point;
let item_j be the second noun;
let iX be the x-value of item_i;
let iY be the y-value of item_i;
let jX be the x-value of item_j;
let jY be the y-value of item_j;
say "[line break]";
say "Coordinates [item_i] : x-value = [iX] y-value = [iY].[line break]";
say "Coordinates [item_j] : x-value = [jX] y-value = [jY].[line break][line break]";
say "Horizontally ";
if iX is not jX:
say "[item_i] is [if iX is less than jX]left[otherwise]right[end if] of [item_j]. [run paragraph on]";
otherwise:
say "[item_i] and [item_j] have the same X value. [run paragraph on]";
say "Vertically ";
if iY is not jY:
say "[item_i] is [if iY is less than jY]under[otherwise]atop[end if] [item_j].[line break]";
otherwise:
say "[item_i] and [item_j] have the same Y value.[line break]";
When running you can explore the properties of the points with each other, examine individual points, and examine the map itself. This is how that looks using the data for the following map:
Demo
In this demo of 2D points you can type "debug map", "examine <point name>", or "compare <point name> to <point name>" to see more information about the 2d point environment.
You can see point_a, point_b, point_c, point_d, point_e, point_f, point_g, point_h, point_i, point_j, point_k, point_l, point_m and point_n here.
>debug map
point_a : x-value = 1, y-value = 0
point_b : x-value = 0, y-value = 0 *** ROOT ***
point_c : x-value = -1, y-value = 0
point_d : x-value = 1, y-value = 1
point_e : x-value = 1, y-value = 2
point_f : x-value = 2, y-value = 0
point_g : x-value = 3, y-value = 0
point_h : x-value = 1, y-value = -1
point_i : x-value = 1, y-value = -2
point_j : x-value = 0, y-value = 1
point_k : x-value = 2, y-value = 1
point_l : x-value = 0, y-value = -1
point_m : x-value = 2, y-value = 2
point_n : x-value = -1, y-value = -1
>compare point_a to point_g
Coordinates point_a : x-value = 1 y-value = 0.
Coordinates point_g : x-value = 3 y-value = 0.
Horizontally point_a is left of point_g. Vertically point_a and point_g have the same Y value.
>compare point_c to point_m
Coordinates point_c : x-value = -1 y-value = 0.
Coordinates point_m : x-value = 2 y-value = 2.
Horizontally point_c is left of point_m. Vertically point_c is under point_m.
>examine point_f
point_f is right of point_a.
point_f is neither atop nor under of point_a.
point_f is neither right nor left of point_b.
point_f is neither atop nor under of point_b.
point_f is neither right nor left of point_c.
point_f is neither atop nor under of point_c.
point_f is neither right nor left of point_d.
point_f is neither atop nor under of point_d.
point_f is neither right nor left of point_e.
point_f is neither atop nor under of point_e.
point_f is neither right nor left of point_f.
point_f is neither atop nor under of point_f.
point_f is left of point_g.
point_f is neither atop nor under of point_g.
point_f is neither right nor left of point_h.
point_f is neither atop nor under of point_h.
point_f is neither right nor left of point_i.
point_f is neither atop nor under of point_i.
point_f is neither right nor left of point_j.
point_f is neither atop nor under of point_j.
point_f is neither right nor left of point_k.
point_f is neither atop nor under of point_k.
point_f is neither right nor left of point_l.
point_f is neither atop nor under of point_l.
point_f is neither right nor left of point_m.
point_f is neither atop nor under of point_m.
point_f is neither right nor left of point_n.
point_f is neither atop nor under of point_n.
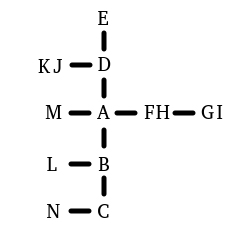
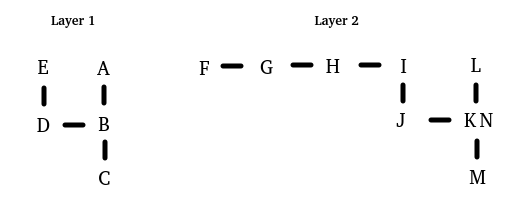
Two other maps were use for testing. One map included cases where multiple points existed in the same locations as other points. The other map had two discrete sets of points that were not connected to each other.
Test Map #2 : (See point definitions below)
>debug map
point_a : x-value = -2, y-value = 0
point_b : x-value = -2, y-value = -1
point_c : x-value = -2, y-value = -2
point_d : x-value = -2, y-value = 1
point_e : x-value = -2, y-value = 2
point_f : x-value = -1, y-value = 0
point_g : x-value = 0, y-value = 0 *** ROOT ***
point_h : x-value = -1, y-value = 0
point_i : x-value = 0, y-value = 0
point_j : x-value = -3, y-value = 1
point_k : x-value = -3, y-value = 1
point_l : x-value = -3, y-value = -1
point_m : x-value = -3, y-value = 0
point_n : x-value = -3, y-value = -2
point_a is atop point_b.
point_b is atop point_c.
point_d is atop point_a.
point_e is atop point_d.
point_f is right of point_a.
point_g is right of point_f.
point_h is right of point_a.
point_i is right of point_h.
point_j is left of point_d.
point_k is left of point_d.
point_l is left of point_b.
point_m is under point_k.
point_n is under point_l.
Test Map #3 : (See point definitions below)
>debug map
point_a : x-value = 0, y-value = 2
point_b : x-value = 0, y-value = 1
point_c : x-value = 0, y-value = 0 *** ROOT ***
point_d : x-value = -1, y-value = 1
point_e : x-value = -1, y-value = 2
point_f : x-value = -4, y-value = 1
point_g : x-value = -3, y-value = 1
point_h : x-value = -2, y-value = 1
point_i : x-value = -1, y-value = 1
point_j : x-value = -1, y-value = 0
point_k : x-value = 0, y-value = 0
point_l : x-value = 0, y-value = 1
point_m : x-value = 0, y-value = -1
point_n : x-value = 0, y-value = 0 *** ROOT ***
point_a is atop point_b.
point_b is atop point_c.
point_d is left of point_b.
point_e is atop point_d.
point_f is left of point_g.
point_g is left of point_h.
point_h is left of point_i.
point_i is atop point_j.
point_j is left of point_k.
point_k is under point_l.
point_m is under point_k.
point_n is under point_l.