Help with shortest path between nodes in Sugarcube 2

[dUrberville]

Twine Version: 2.8.1

Hello, I’m developing an open world text based game where travel is mainly done between settlements (nodes) on a map. I’m trying to figure out how to make it so I can choose a destination node and calculate the shortest path from the current node to there. I think without this feature travel will be a huge hassle, so it’s high on the priority list.

The problem is I’m not much of a math guy, or a coder, so I’m really struggling to understand how to implement this. I only learned about the Dijkstra algorithm (which is what games use to accomplish this) while trying to implement this, but I don’t really understand it well enough to code it. I’ve tried ChatGPT help or studying the algorithm step by step, but I just don’t get it. Also, I don’t know javascript, so I’ve been trying to do it solely with TwineScript.

So, it’s a bit of an ask, but can someone help me implement this? It seems to me to be the most ‘real code’ part of my game.

Here’s where I’m at right now. I’m initializing the map, starting small with example A-E names until I can get this working. This includes connections between nodes and distances.

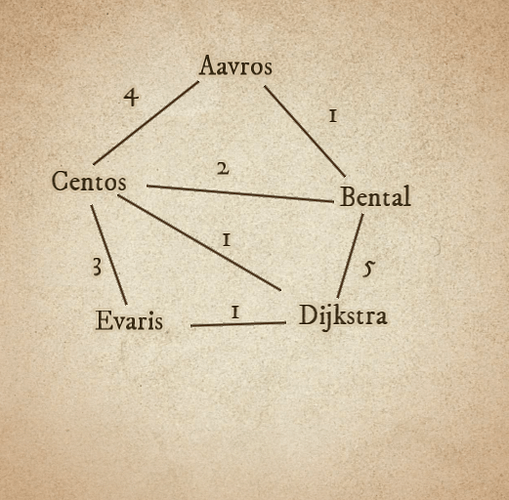
<<set $currentPlace = "Aavros">>
<<set $destination = "Evaris">>
<<set $shortestPath = []>>

<<set $places to {
    "Aavros": { "neighbors": {"Bental": 1, "Centos": 4}},
    "Bental": { "neighbors": {"Aavros": 1, "Centos": 2, "Dijkstra": 5}},
    "Centos": { "neighbors": {"Aavros": 4, "Bental": 2, "Dijkstra": 1, "Evaris": 3}},
    "Dijkstra": { "neighbors": {"Bental": 5, "Centos": 1, "Evaris": 1}},
    "Evaris": { "neighbors": {"Centos": 3, "Dijkstra": 1}}
}>>

And that’s really all I’ve got. I tried multiple ways to implement the Dijkstra algorithm into a widget according to what ChatGPT would say, but of course it was riddled with errors and I didn’t have enough of a grasp of what was going on to fix them.

Here’s a graph I put together while trying to figure it out, if that might help someone put this together.

I’d appreciate any assistance.

[Hituro (David Donachie)]

Step one would be, don’t use a <<widget>>. Widgets are slow (because of the overhead of processing all the macros) compared to raw JS, what you want is a JS function.

Secondly, I don’t know that you need Djikstra’s, but it depends on the size of your map. If your map is small, a simple Depth First Search will do what you need. Even if you do need Djikstra’s, it might be easier for you mentally to do the DFS first, and then see how it is optimised to become a faster algorithm if you need it.

The basic outline of what you need to do is:

• Create an empty array of nodes to check
• Create an empty array of nodes already checked
• Create an empty array of successful routes
• Create a number (0) of the distance down the current path
• Start at the beginning and put each of the next nodes on the list in some order
• Take a node off the list:
  • if it is in the already visited list, discard it.
  • if not record the distance travelled, check to see if it is the target. If it is, record it in your list of solutions
• then go on to the next node on the list.
• When you run out of nodes, pick the shortest route from your solutions

This is from memory, take with a certain pinch of salt

If that’s still too slow you can start optimising, like you can discard any route if the current distance is greater than the best already recorded, and you can use a heuristic (now we are in Djikstra’s et. al. territory) to pick the best node to pick next.

[Hituro (David Donachie)]

I was going to leave it there, with some homilies and a bad DFS implementation, but the more I thought about it, the more my 2nd post was less than useful, so I will start over.

First the homilies

• A process of graph search like this can take a long time, theoretically exponential time, depending on complexity.
• You can reduce this by calculating the possible routes ahead of time and only storing those in your game. Depending on the number of locations this may be less overhead than searching the tree live
• The lower end the device in terms of processing, the more you will find pre-calculation better

That said, after having written my own weighted DFS for your data, I decided to just skip ahead to a Djikstra’s implementation anyway, and I think it’s probably best, since you really want the shortest route (not merely a short route) and also may have a big graph.

To implement Djikstra’s you need a queue that is sorted by priority, so you can get the best next node to look at all the time. So that’s the first thing:

class PriorityQueue {
  constructor() {
    this.collection = [];
  }
  
  enqueue(element){
    if (this.isEmpty()){ 
      this.collection.push(element);
    } else {
      let added = false;
      for (let i = 1; i <= this.collection.length; i++){
        if (element.dist < this.collection[i-1].dist){ 
          this.collection.splice(i-1, 0, element);
          added = true;
          break;
        }
      }
      if (!added){
          this.collection.push(element);
      }
    }
  };
  
  dequeue() {
    let value = this.collection.shift();
    return value;
  };  
  
  isEmpty() {
    return (this.collection.length === 0) 
  };
}

(courtesy of adriennetjohnson on medium)

Once you have a queue, the Djikstra’s algorithm is basically a process of:

• Set the initial cost of reaching any node (distance in your case) to Infinity
• Set an empty list of paths to each node
• Starting at the origin, consider each child node of the current node
  • calculate the distance to that node through the current one (distance to the current node + distance to the child)
  • If that’s better than the distance you currently have for the node (i.e. this is a better route), update your list of paths to say that currentNode => child is the best path, and update your distance
  • put the child in the queue

Once this process is finished, the list of distances shows the total distance to the destination, and the list of paths allows you to backtrack your way up the shortest links to the origin.

setup.djikstra = function() {
    const start   = State.variables.currentPlace;
    const dest    = State.variables.destination;
    const tree    = State.variables.places;
    const dists   = {};
    const path    = {};
    const pq      = new PriorityQueue();
    
    // initialise distances
    for (const node in tree) {
      dists[node] = Infinity;
    }
    dists[start] = 0;
    
    // initialise queue with start
    pq.enqueue({ node: start, dist: 0 });
    
    // calculate best distances in the tree
    while (!pq.isEmpty()) {
      let curr = pq.dequeue();
      
      for (const child in tree[curr.node].neighbors) {
        let dist = dists[curr.node] + tree[curr.node].neighbors[child];
        if (dist < dists[child]) {
          dists[child] = dist;
          path[child] = curr.node;
          pq.enqueue({ node: child, dist: dist });
        }
      }
    }
    
    // calculate the best route to dest
    let route = [dest];
    let last = dest;
    while (last !== start) {
      route.unshift(path[last]);
        last = path[last];
    }
    
    return { route: rotue, dist: dists[dest] }
}

[jkj_yuio]

Each node has a visited marker. They all start blank.

Put the start node into an array and mark it visited.
set position to zero
loop:
take node at position. if its the destination, stop.
find all nonvisited exits from node, add to end of array. Mark them visited.
increment position.
end loop

A bit more housekeeping collects path.

[dUrberville]

Thank you both. I was able to implement the first answer successfully. Cheers!