Well, I think this works! At least for relatively small values of N. (“N” in the following means the total number of people in the puzzle.)
First, let’s define our parameters. I’m making them global variables so we can tweak them later, but they should always be constant within a puzzle.
(global variable (total number of people 3))
(global variable (number of knaves 2))
(number of knights $Knights)
(total number of people $Total)
(number of knaves $Knaves)
($Total minus $Knaves into $Knights)
(total number of people squared $Square)
(total number of people $Total)
($Total times $Total into $Square)
(global variable (number of statements 4))
Since we can’t make multidimensional arrays, we fake it with a big list. If X is making a statement about Y, then we’ll store a 1 at X×N+Y. Otherwise, we’ll store a 0 there.
Note that looking up a value in this list is O(N²), which is not great. We’ll want to keep N fairly small.
(complete graph $G)
(total number of people squared $N)
($N instances of 1 into $G)
(0 instances of $ into [])
($N instances of $Value into [$Value|$Tail])
($N minus 1 into $Nm1)
($Nm1 instances of $Value into $Tail)
(convert $In to index $Out) %% Convenience predicate for coordinate conversion
(if) ($In = [$X $Y]) (then) %% Coordinates are 0-indexed to make the math easier
(total number of people $N)
($X times $N into $Tmp)
($Tmp plus $Y into $Tmp2)
($Tmp2 plus 1 into $Out) %% Add 1 because lists in Dialog are 1-indexed
(else)
($In = $Out)
(endif)
We could make the coordinate conversion a bit more efficient by passing X and Y separately instead of using a list, but I’m more worried about readability than efficiency here.
Notably, though, we don’t want to start with a complete graph—statements like “Alice says Alice is a knight” are completely worthless! So we remove the diagonal elements from it.
(remove diagonals from $In into $Out)
(total number of people $Total)
(remove $Total diagonals from $In into $Out)
(remove 0 diagonals from $In into $In) %% We're done
(remove $N diagonals from $In into $Out)
($N minus 1 into $Nm1)
(convert [$Nm1 $Nm1] to index $Index)
(change entry $Index of $In to 0 into $Tmp)
(remove $Nm1 diagonals from $Tmp into $Out)
To modify the list, we’ll use these predicates. (The standard library also provides these as “nth” and “replace nth” but I didn’t know about the latter until I had already written these, and they have more readable names besides.)
(change entry 1 of [$|$Tail] to $Value into [$Value|$Tail])
(change entry $N of [$Head|$Tail] to $Value into [$Head|$NewTail])
($N minus 1 into $Nm1)
(change entry $Nm1 of $Tail to $Value into $NewTail)
(entry 1 of [$Head | $] into $Head)
(entry $N of [$ | $Tail] into $Value)
($N minus 1 into $Nm1)
(entry $Nm1 of $Tail into $Value)
Now, since we’re using indices instead of objects for our knights and knaves, we need a new way to iterate over them. This is what I’m currently using.
(have $N count up from $Low to $High)
($N = $Low)
(or)
($Low plus 1 into $Lp1)
~($Lp1 > $High)
*(have $N count up from $Lp1 to $High)
(person index $N)
(total number of people $Total)
($Total minus 1 into $Tm1)
*(have $N count up from 0 to $Tm1)
Note that our person indices start at zero rather than one! Not a great decision, honestly.
Now, we’re storing this as a directed graph, where “Alice makes a statement about Bob” is separate from “Bob makes a statement about Alice”. But when we check if it’s connected, we want to treat it as an undirected graph, where those two are equivalent. So we have a different way of looking up values for that!
(connection between $X and $Y in $G)
(if) ~(fully bound $Y) (then) %% Make sure it iterates over the right range if it's unbound
*(person index $Y)
(internal connection between $X and $Y in $G)
(else)
(internal connection between $X and $Y in $G)
(endif)
(internal connection between $X and $Y in $G)
(convert [$X $Y] to index $Idx1)
(entry $Idx1 of $G into 1)
(or)
(convert [$Y $X] to index $Idx2)
(entry $Idx2 of $G into 1)
Note that, if $Y is unbound, we iterate over all person-indices, not over all objects or numbers.
To determine if the graph is connected, we just do a floodfill. If the flood touches every person, the graph is connected.
($List contains all people)
(length of $List into $N)
(total number of people $N)
(flood $ from $LastGen) %% End recursion in success when we've hit everything
($LastGen contains all people)
(flood $G from $LastGen)
(collect $NextStep)
*($LastStep is one of $LastGen)
*(connection between $LastStep and $NextStep in $G)
(into $NextSteps)
(fully bound $NextSteps)
(append $LastGen $NextSteps $NextGenRaw)
(remove duplicates $NextGenRaw $NextGen)
(length of $LastGen into $Old)
(length of $NextGen into $New)
~($Old = $New) %% If we've made no progress, fail
(flood $G from $NextGen)
(connected $G)
(flood $G from [0]) %% Arbitrary starting point
That’s not the only condition, though: for the sake of having an interesting puzzle, we also want everyone to make at least one statement. We’ll need a quick utility predicate for this:
(drop 0 from $List into $List)
(drop $N from [$|$OldTail] into $NewTail)
($N minus 1 into $Nm1)
(drop $Nm1 from $OldTail into $NewTail)
Now we can check if someone’s row in the matrix is completely empty.
($Person gives no testimony in $G)
(total number of people $Total)
($Total times $Person into $Prefix)
%% Now $Prefix is the number of entries to discard before our person's row
(drop $Prefix from $G into $Tmp)
%% And $Total is the number of entries in this person's row
(take $Total from $Tmp into $Row)
%% Now we need to check if $Row contains anything
(accumulate $Entry)
*($Entry is one of $Row)
(into 0) %% If it contains nothing at all, then they give no testimony
Why do we design the predicate this way (checking for no testimony instead of for any testimony)? Well, because Dialog’s multiqueries make it easy to test if a predicate is true for any thing, but very hard to test if a predicate is true for all things.
(someone gives no testimony in $G)
*(person index $Person)
($Person gives no testimony in $G)
We use an access predicate to flip it around to work the intuitive way, though.
@(valid testimony $G)
~(someone gives no testimony in $G)
Now, we want to randomly discard connections from the graph until we have the appropriate number of statements. We’re specifically not trying to detect loops or anything—if we were, generating a tree is significantly easier than what we’re doing! (All we’d have to do is give each node a random parent.) But having loops is useful, puzzle-wise: it gives the player a way to confirm their deductions by adding some redundancy.
(count connections from $G into $Count)
(accumulate $Conn)
*($Conn is one of $G)
(into $Count)
To randomly drop a connection, first we need to determine all ways to drop a connection.
(remove one connection from [0 | $OldRest] into [0 | $NewRest])
*(remove one connection from $OldRest into $NewRest)
(remove one connection from [1 | $OldRest] into [0 | $OldRest])
(remove one connection from [1 | $OldRest] into [1 | $NewRest])
*(remove one connection from $OldRest into $NewRest)
Now we pick one of them at random—specifically, one that leaves the graph connected and valid. This takes O(N⁴) space, which is really not good.
(randomly remove one connection from $G into $G2)
(collect $New)
*(remove one connection from $G into $New)
(connected $New)
(valid testimony $New)
(into $Options)
(randomly select $G2 from $Options)
Do this over and over until we have the number of connections we want.
(trim $G to $N connections into $G)
(count connections from $G into $N)
(trim $G to $N connections into $G2)
(randomly remove one connection from $G into $Tmp)
(trim $Tmp to $N connections into $G2)
And putting it all together:
(generate puzzle $G)
(complete graph $Start)
(remove diagonals from $Start into $Next)
(number of statements $N)
(trim $Next to $N connections into $G)
To choose our knaves, we need another little utility predicate.
(select knaves into $Knaves)
(collect $Index)
*(person index $Index)
(into $Options)
(number of knaves $N)
(randomly select $N from $Options without replacement into $Knaves)
(randomly select 0 from $ without replacement into [])
(randomly select $N from $List without replacement into [$Chosen|$MoreChosen])
(randomly select $Chosen from $List)
(split $List by $Chosen into $Left and $Right)
(append $Left $Right $Shrunken)
($N minus 1 into $Nm1)
(randomly select $Nm1 from $Shrunken without replacement into $MoreChosen)
Now all we have to do is print the statements!
(name for index $Index)
($Index plus 1 into $Ip1) %% Our person indices go from zero, Dialog lists go from one
(entry $Ip1 of [Alice Bob Claire Dave Emma Fred Gwen Harry Isabelle Jake Kyra Liam Mary Nick Olivia Pedro] into $Name)
(uppercase) $Name
If they’re both of the same type—knight on knight, knave on knave—it’s an affirmation. Otherwise, it’s an accusation. I feel like there should really be a more elegant way to XOR two conditions in Dialog, but if there is, I don’t know it.
(statement from $Source about $Target with knaves $Knaves)
(if) ($Source is one of $Knaves) (then)
($SourceGuilty = 1)
(else)
($SourceGuilty = 0)
(endif)
(if) ($Target is one of $Knaves) (then)
($TargetGuilty = 1)
(else)
($TargetGuilty = 0)
(endif)
(if) ($SourceGuilty = $TargetGuilty) (then)
($Source affirms $Target)
(else)
($Source accuses $Target)
(endif)
An “affirmation” is saying someone’s a knight; an “accusation” is saying someone’s a knave.
($Source affirms $Target)
(name for index $Source) says: "(no space)(name for index $Target) is innocent!"
($Source accuses $Target)
(name for index $Source) says: "(no space)(name for index $Target) is guilty!"
Now we can just present all the statements in a list. But we need one more caveat: if the number of knights is equal to the number of knaves, then the solution is not unique! Affirmations and accusations tell us whether people are the same type or different types, but neither of them actually tells us whether someone is a knight or a knave.
So in this case, we add one more piece of evidence. Since I’ve been playing Ace Attorney recently, I’ve (minimally) flavored this as suspects on trial.
(present puzzle $G with knaves $Knaves)
(total number of people $Total)
(number of knaves $Guilty)
$Total people have been accused of a crime! $Guilty of them (if) ($Guilty = 1) (then) is (else) are (endif) actually guilty. The innocent will tell the truth, the guilty will lie.
(exhaust) {
*(person index $Source)
*(person index $Target)
(convert [$Source $Target] to index $Index)
(entry $Index of $G into 1)
(line) (statement from $Source about $Target with knaves $Knaves)
}
(if) (number of knights $N) (number of knaves $N) (then) %% This is the only case where there's a legitimate ambiguity
(par) You also have conclusive evidence that (name for index 0) is
(if) (0 is one of $Knaves) (then) guilty (else) innocent (endif)
.
(endif)
Finally, we add a very minimal user interface to let people generate puzzles. (Really the minimum number of connections is N-1, not N, which I didn’t realize until I already posted this, but that’s an easy change.)
(program entry point)
How many knights should there be in the puzzle?
(get number $Knights)
(par) How many knaves should there be in the puzzle?
(get number $Knaves)
(now) (number of knaves $Knaves)
($Knights plus $Knaves into $Total)
(now) (total number of people $Total)
(par) How many statements should there be?
(get number $Evidence)
(if) ($Evidence < $Total) (then) Error: evidence cannot be < knights + knaves! (fail) (endif) %% Avoid a crash if this happens
(now) (number of statements $Evidence)
(generate puzzle $G)
(select knaves into $KnaveList)
(par) (present puzzle $G with knaves $KnaveList)
(par) Press ENTER to see the solution.
(get input $)
Knaves:
(exhaust) {
*($Knave is one of $KnaveList)
(name for index $Knave)
}
(get number $N)
*(repeat forever)
> (get input $Words)
{
($Words = [$N]) (number $N)
(or)
That is not a number. (line) (fail)
}
And while we’re not using the standard library, we do need some of the list-manipulation predicates from it, so I’ve copied those here.
(interface (remove duplicates $<Input $>Output))
(remove duplicates [] [])
(just)
(remove duplicates [$Head | $MoreIn] $MoreOut)
($Head is one of $MoreIn)
(just)
(remove duplicates $MoreIn $MoreOut)
(remove duplicates [$Head | $MoreIn] [$Head | $MoreOut])
(remove duplicates $MoreIn $MoreOut)
(interface (length of $List into $>Number))
(length of [] into 0)
(length of [$ | $More] into $Np1)
(length of $More into $N)
($N plus 1 into $Np1)
(interface (nth $List $<Index $Element))
(nth [$Head | $] 1 $Head)
(nth [$ | $Tail] $N $Result)
($N minus 1 into $Nm1)
(nth $Tail $Nm1 $Result)
(interface (randomly select $>Element from $<List))
(randomly select $Element from $List)
(length of $List into $N)
(random from 1 to $N into $Index)
(nth $List $Index $Element)
(take 0 from $ into [])
(take $N from [$Head | $MoreIn] into [$Head | $MoreOut])
($N minus 1 into $Nm1)
(take $Nm1 from $MoreIn into $MoreOut)
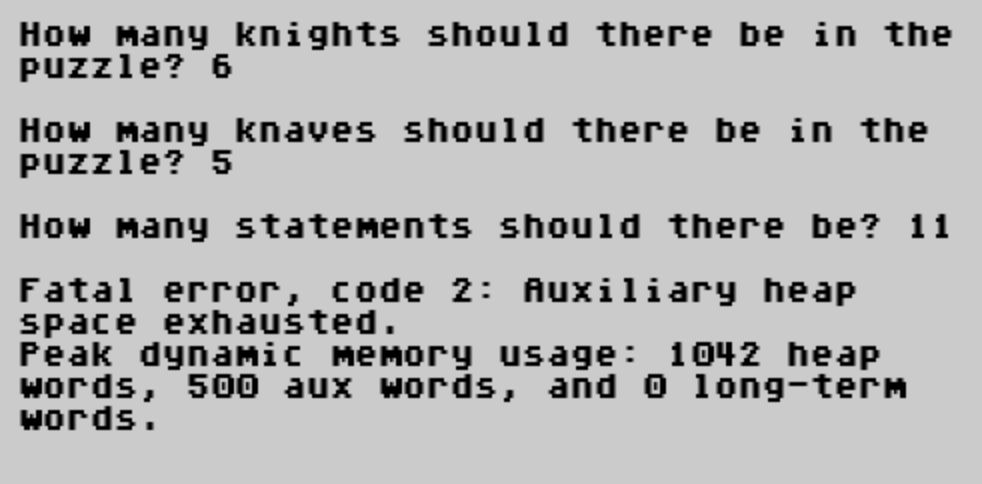
Now you can play the whole thing in dgdebug. You can’t, unfortunately, play it in the Z-machine—at least for more than a trivial number of suspects. It just uses too much memory. I’m not sure if that’s a problem that can be solved; Dialog list-manipulation is just too slow and inefficient. But there are definitely some ways to cut down the O(N⁴) memory usage, like storing the index of the removed connection instead of the entire modified graph when choosing one at random (which would take it down to O(N²)). If you want to use this in an actual game, I recommend doing that.
knaves.dg (10.7 KB)
Run with dgdebug knaves.dg, no library necessary. And if you want to try the puzzles, here are some example outputs:
3 people have been accused of a crime! 1 of them is actually guilty. The innocent will tell the truth, the guilty will lie.
Alice says: “Bob is guilty!”
Alice says: “Claire is innocent!”
Bob says: “Alice is guilty!”
Claire says: “Alice is innocent!”
Knaves: |_|_Bob_|_|
5 people have been accused of a crime! 2 of them are actually guilty. The innocent will tell the truth, the guilty will lie.
Alice says: “Dave is innocent!”
Bob says: “Claire is innocent!”
Claire says: “Alice is guilty!”
Claire says: “Dave is guilty!”
Dave says: “Claire is guilty!”
Dave says: “Emma is innocent!”
Emma says: “Bob is guilty!”
Knaves: Bob Claire
5 people have been accused of a crime! 2 of them are actually guilty. The innocent will tell the truth, the guilty will lie.
Alice says: “Bob is guilty!”
Alice says: “Dave is guilty!”
Bob says: “Alice is guilty!”
Claire says: “Dave is guilty!”
Dave says: “Claire is guilty!”
Dave says: “Emma is guilty!”
Emma says: “Claire is innocent!”
Knaves: Dave Bob
6 people have been accused of a crime! 3 of them are actually guilty. The innocent will tell the truth, the guilty will lie.
Alice says: “Dave is innocent!”
Bob says: “Emma is guilty!”
Claire says: “Fred is innocent!”
Dave says: “Claire is guilty!”
Dave says: “Fred is guilty!”
Emma says: “Claire is guilty!”
Emma says: “Fred is guilty!”
Fred says: “Emma is guilty!”
You also have conclusive evidence that Alice is guilty.
Knaves: Dave Alice Emma