Okay, I literally got my PhD in this field (topology).
A surface like this has two kinds of coordinates, intrinsic and extrinsic.
Extrinsic coordinates are the coordinates of the bigger space you’ve put the surface in. An example would be a ghost, unaffected by gravity, floating around and through the earth. They have 3 natural directions of movement, even though the face of the earth is only 2-dimensional.
Intrinsic coordinates are the coordinates of the space itself viewed from ‘inside’. For example, on our earth some intrinsic coordinates are latitude and longitude.
Generally, from a math perspective, intrinsic coordinates are strongly preferred. People living in a manifold don’t even know they’re in a manifold. The secret is there may not be any outside space. Space can be curved, yes, but it doesn’t have to be curved in something larger.
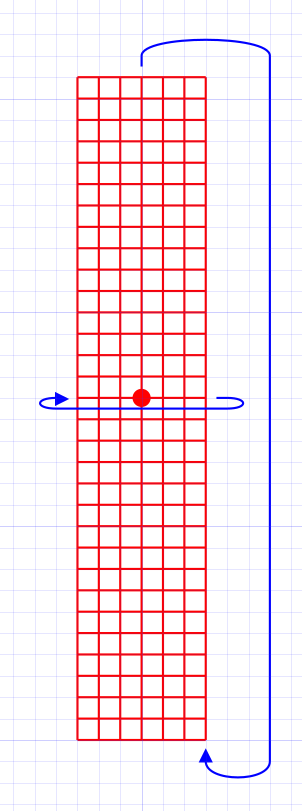
With intrinsic coordinates on a ‘flat’ klein bottle (a square where going off one edge teleports you to another, with a ‘reflection’ when teleporting from north to south but not from east to west), all you would see around you is an infinite repeating chessboard-like pattern, where everything on one ‘color’ of squares (say, white) would be oriented the same way as you and the other color would be flipped. But you wouldn’t actually see any hard boundaries between the two. There would be an infinite grid of yourself, half of them flipped, half not.
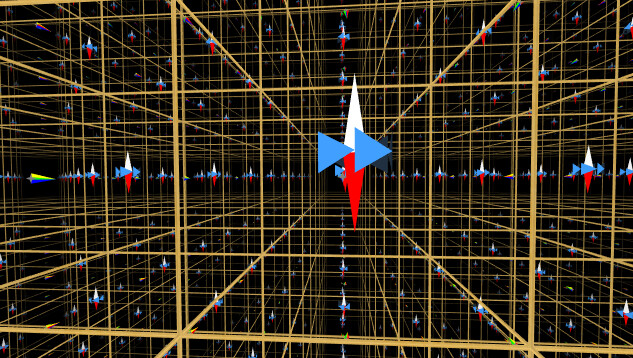
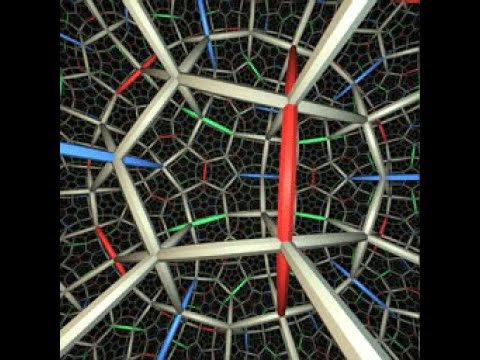
The website Geometry Games has little simulators allowing you to see what living in a curved space would be like.
If my understanding of the Klein bottle is correct, my perpective would be analogous to what a flatlander would see when a rectangle is entirely perpendicular to the plane the flatlander lives in. In other words, I would not be able to see anything at all because my three-dimensional eyes would not be able to see my home from the necessary angle.
This is true if using extrinsic coordinates. It is not true when using intrinsic coordinates.
Editedit:
It would look a bit like this, but only one ‘plain’. This is more of a 3d version with layers of klein bottles stacked on each other or where going up loops with going down. This is from that game I linked:
Also, if you want to be a 3d person walking on a klein bottle, you could just take a 3d space called ‘the klein bottle crossed with an interval’. This just ‘thickens’ the klein bottle to make it 3d, much like the atmosphere on our earth’s crust makes it a ‘sphere cross an interval’ rather than a truly 2-dimensional sphere.
Editeditedit: Also I highly recommend this film to people who want to understand what walking around in these spaces is like: